
Essays |
The
Maximum
Profit
Point
by Michael T. Martin
|
We have seen up to this point that consumers alone determine the maximum amount of spending (Rmax) that any marketplace will offer to suppliers. Because consumers have choices, and because those choices are influenced by price, and because consumers only have a finite amount of money available to spend, they exhibit behavior in a marketplace that we call a demand curve that produces only a single combination of price and quantity that will induce them to spend all of the money they have (Rmax). Suppliers are perfectly willing to sell to consumers but they have the overriding specter of costs to consider. The interrelationship between fixed and variable costs presents a complex conundrum to suppliers in the marketplace. The region of profits available to suppliers exists only in a lens shaped zone where profits may be very small or very large. Suppliers can control the quantity of sales, and therefore the point of profits, by changing prices. Consumers have a demand curve that is independent of supplier's costs: consumers react to their own gratification based on competing wants and choices, but that demand curve will react to prices and produce quantities sold that determine the total cost curve, and hence total profits.
If you look at the (blue) total cost curve, it has either a constant or near constant slope. The total revenue curve (green), however, starts with a very very low slope at zero quantity and then as volume rises the slope becomes near vertical before it tops out and becomes horizontal again at Rmax. At any point where the slope of the total revenue curve is higher (steeper) than the slope of the total cost curve, it means revenues are increasing faster than costs and total profits are increasing as volume increases. At any point where the slope of the total revenue curve is lower than the slope of the total cost curve, it means costs are rising faster than revenues and thus profits are decreasing as volume increases. At precisely the point where the slope of the total revenue curve exactly equals the slope of the total cost curve, we have the point of maximum profits: any quantity of sales above or below produces lower total profits. Thus we only have to look at the chart to find where the total revenue curve slope exactly equals the total cost curve slope and are parallel: meaning the slopes are the same. And that is where the dashed blue line that has exactly the same slope as the variable cost curve is moved to be tangent to the green total revenue curve. At this point of tangency we have maximum profits. Let us call this $max because this is where the seller makes the most money. Now looking at the chart that shows both total revenue and total cost curves, it becomes obvious that the slope of the total revenue curve is zero at Rmax and therefore the point of $max must occur at a lower volume than the volume at Rmax. In other words, no seller will conscientiously attempt to sell at a price that takes all of the money consumers are willing and able to spend, because that point is at Rmax which is not the point of $max where the seller gets the most money in profits. The sellers will nearly always strive to reach $max and this point of maximum profits is necessarily always at a higher price (and lower quantity) than the price that produces maximum revenues. Which also necessarily means that no matter how willing consumers are to spend, they will always be forced to save some of their money because sellers simply won't want to sell at the price where consumers are willing to spend all their money. Notice also that to more clearly show the difference between $max and Rmax, we increased the slope of the variable cost curve - meaning it cost more per item to produce - which moved the point of $max to the left and away from Rmax. In other words, the more inefficient the technology in use, the greater the difference between $max and Rmax, which also corresponds to a greater amount of savings consumers are forced to have. This greater pool of savings is therefore available to invest in new technology. However, it is also, ipso facto, true that higher technology markets will save less than lower technology markets. Indeed, if technology becomes extremely efficient the degree of consumer savings will virtually disappear as the point of $max approaches the point of Rmax. On the other hand, it is a myth that businesses will always try to raise prices. Even without competition, the point of maximum profits would be the highest price that a business would attempt to charge. To charge either a higher or lower price would mean lower profits. There is no escaping this conclusion: as long as consumers switch preferences if prices change and costs increase with production increases (even if the cost-per-item stays constant), there will be a price where sellers maximize their total profits while still leaving consumers some money left over to save. Introduction | Previous | Next: How Costs Affect Profits
|
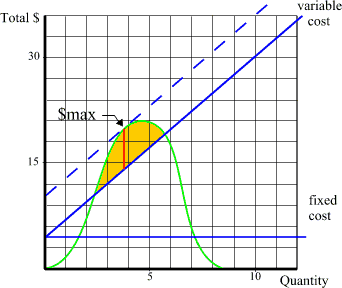 Naturally, the vertical difference between the total revenue curve and the total cost curve represents profits to the business. Therefore, this graph demonstrates that profits will be zero or negative (losses) at both high and low volumes while in between they will rise to some point of maximum profits (red line). The question is to determine where the point of maximum profits exists, and the answer is simple.
Naturally, the vertical difference between the total revenue curve and the total cost curve represents profits to the business. Therefore, this graph demonstrates that profits will be zero or negative (losses) at both high and low volumes while in between they will rise to some point of maximum profits (red line). The question is to determine where the point of maximum profits exists, and the answer is simple.